Welcome to Workshop on Applied Mathematics and Graph Theory
The Workshop on Applied Mathematics and Graph Theory brings together researchers, academics, and practitioners to discuss recent advances in applied mathematics, graph theory, combinatorics, network science, and related fields. Held annually in Ohrid during August.
Call for Papers
Find information about paper submission guidelines, important dates, and topics of interest for the workshop. This section provides everything you need to know to submit your research for presentation.
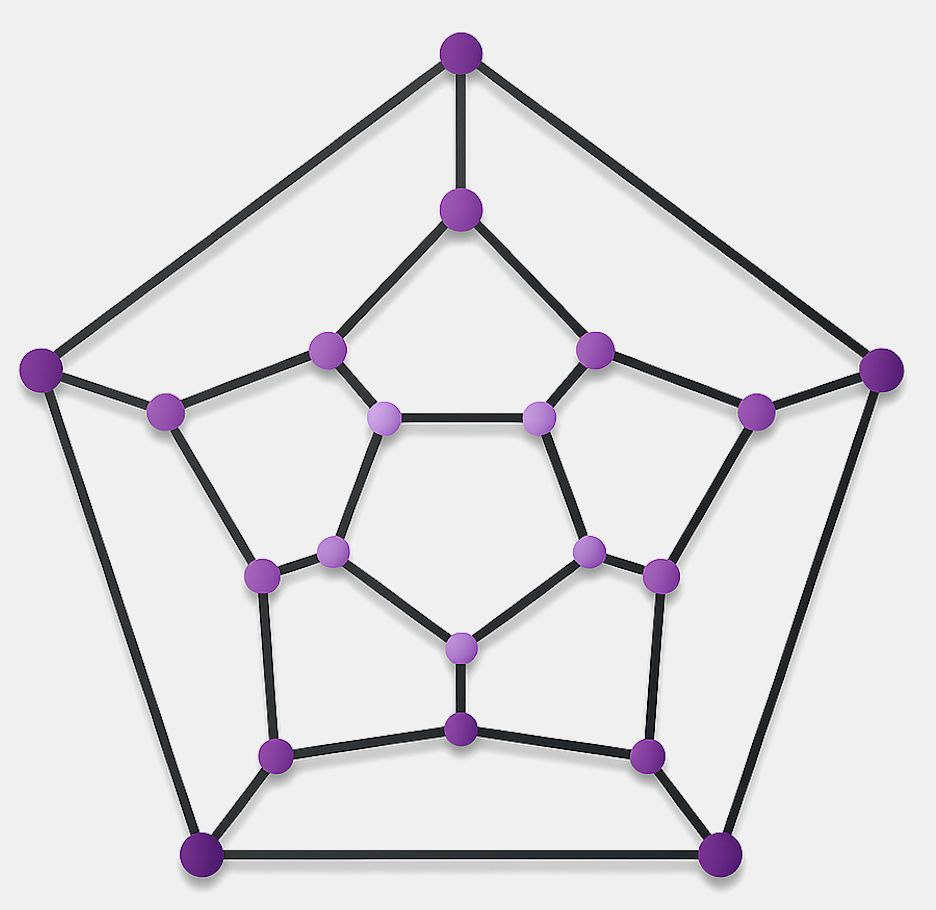
Classical Result in Graph Theory
Euler's Formula for Planar Graphs
Euler’s Formula for Planar Graphs
Theorem
For any connected planar graph drawn without edge intersections:
$$V - E + F = 2$$where $V$ is the number of vertices, $E$ the number of edges, and $F$ the number of faces (including the outer face).
Proof Sketch
The proof proceeds by induction on the number of edges. For a tree ($F=1$), we have $E = V-1$, so $V - (V-1) + 1 = 2$. Adding an edge while maintaining planarity increases both $E$ and $F$ by 1, preserving the equality.
Applications
- Proves that $K_5$ and $K_{3,3}$ are non-planar
- Yields the inequality $E \le 3V - 6$ for $V \ge 3$
- Foundation for the Four Color Theorem
Historical Context
Discovered by Leonhard Euler in 1752 while studying polyhedra, this formula marked the birth of topological graph theory.